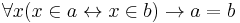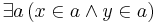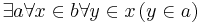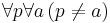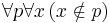Kripke–Platek set theory with urelements
The Kripke–Platek set theory with urelements (KPU) is an axiom system for set theory with urelements that is considerably weaker than the familiar system ZF.
Contents |
Preliminaries
The usual way of stating the axioms presumes a two sorted first order language 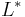 with a single binary relation symbol
with a single binary relation symbol  . Letters of the sort
. Letters of the sort 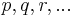 designate urelements, of which there may be none, whereas letters of the sort
designate urelements, of which there may be none, whereas letters of the sort 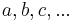 designate sets. The letters
designate sets. The letters 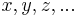 may denote both sets and urelements.
may denote both sets and urelements.
The letters for sets may appear on both sides of  , while those for urelements may only appear on the left, i.e. the following are examples of valid expressions:
, while those for urelements may only appear on the left, i.e. the following are examples of valid expressions: 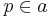 ,
, 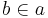 .
.
The statement of the axioms also requires reference to a certain collection of formulae called 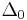 -formulae. The collection
-formulae. The collection 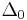 consists of those formulae that can be built using the constants,
consists of those formulae that can be built using the constants,  ,
, 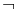 ,
, 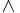 ,
, 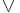 , and bounded quantification. That is quantification of the form
, and bounded quantification. That is quantification of the form 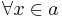 or
or 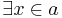 where
where  is given set.
is given set.
Axioms
The axioms of KPU are the universal closures of the following formulae:
- Foundation: This is an axiom schema where for every formula
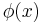 we have
we have 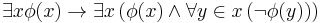 .
.
- Δ0-Separation: This is again an axiom schema, where for every
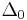 -formula
-formula 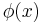 we have the following
we have the following 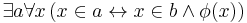 .
.
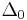 -Collection: This is also an axiom schema, for every
-Collection: This is also an axiom schema, for every 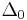 -formula
-formula 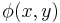 we have
we have 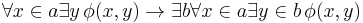 .
.
- Set Existence:
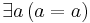
Additional assumptions
Technically these are axioms that describe the partition of objects into sets and urelements.
Applications
KPU can be applied to the model theory of infinitary languages. Models of KPU considered as sets inside a maximal universe that are transitive as such are called admissible sets.
See also
References
- Gostanian, Richard, 1980, "Constructible Models of Subsystems of ZF," Journal of Symbolic Logic 45 (2): .
- Jon Barwise, Admissible Sets and Structures. Springer Verlag. ISBN 3540074511